1. Uvod

U jedanaestom mjesecu aktivnosti 1 nastavlja se rad na analizi dostupne literature o postojećim metodologijama za procjenu rizika od potresa. U ovom je razdoblju detaljnije prikazana odabrana metoda analize i evaluacije rizika koja se pokazala kao vrlo pogodna za procjenu rizika od potresa. Naime, u slučaju kad ne postoji dovoljno veliki broj ulaznih podataka, metoda analitičkog hijerarhijskog procesa (engl. analytic hierarchy process - AHP) pokazala se vrlo točnom i prikladnom za procjenu rizika.

2. Analitički hijerarhijski proces

Analitički hijerarhijski proces (AHP) spada u metodu višekriterijalnih analiza koja objedinjuje kvantitativne i kvalitativne podatke s ciljem donošenja odluka u definiranju prioriteta alternativnih rješenja određenog problema. Posebno je pogodna u slučajevima kada ne raspolažemo s dovoljnim brojem statističkih podataka, odnosno kada gotovo sve komponente rizika nisu mjerljive ili imaju vrlo visok stupanj nesigurnosti. U slučaju potresnog  rizika prisutne su spomenute komponente, te je stoga AHP pogodna i široko primjenjiva metoda za njegovu procjenu. Primjena AHP metode u potresnim rizicima se može pronaći u mnogim znanstvenim radovima, te studijama slučajeva praktičnih primjera.
U nastavku ovog izvješća detaljnije je opisan AHP te su dani primjeri njegove primjene za procjenu potresnog rizika.

2.1 Opis metode

AHP je metoda koja služi kao pomoć u odlučivanju, a rezultira prioritetima različitih alternativnih opcija uspoređivanim prema složenim ili višestrukim kriterijima. Jednostavnim usporedbama parova elemenata modela, AHP-om se dobiva težinska vrijednost pojedine alternativne opcije. Vrijednosti za usporedbu mogu se dobiti stvarnim ili relativnim mjerenjima, ili pak subjektivnim procjenama stručnjaka s velikim iskustvom.
Metoda AHP-a predstavlja nadogradnju metode jednostavnog zbrajanja težina (engl. simple additive weighting - SAW). AHP je razvio Thomas L. Saaty kao pomoć kod donošenja odluka (Saaty, 1992; Saaty, 1994; Saaty i Alexander, 1989). Metoda je aktualna i primijenjena na brojnim konkretnim primjerima kod raznih vrsta donošenja odluka. Inkorporirajući subjektivne procjene i objektivne činjenice u logičan hijerarhijski okvir AHP omogućuje donositelju odluka intuitivan i logičan  pristup za kvantificiranje važnosti svakog elementa alternativne odluke kroz proces međusobnog uspoređivanja. Ovaj proces omogućuje donositeljima odluka da kompleksan problem svedu na hijerarhijsku formu koja ima više razina, a minimalno tri: cilj analize, kriteriji i alternative.

Proces započinje determiniranjem relativne važnosti pojedinih kriterija u postizanju cilja.  Zatim se vrši uspoređivanje alternativa s obzirom na svaki zadani kriterij, da bi se dobila relativna važnost jedne alternative u odnosu na drugu.  Konačno se rezultati te dvije analize sintetiziraju da se izračuna relativna važnost alternativa u odnosu na postizanje cilja.
Proces uspoređivanja reprezentira se formiranjem usporedne matrice. Ako na raspolaganju ima n kriterija, odnosno alternativa koji formiraju usporednu matricu, potrebno je napraviti n(n-1)/2 prosudbi, odnosno usporedbi. Svojstveni vektor svake usporedne matrice predstavlja rang listu prioriteta, dok svojstvena vrijednost daje mjeru konzistencije kojom je vršena prosudba odnosno usporedba.  Sintetizirani svojstveni vektor predstavlja globalni poredak alternativa u odnosu na postizanje cilja. Globalni koeficijent konzistencije manji od 0.10 je prihvatljiv, inače je potrebno vršiti reviziju prosudbi koje su napravljene.

2.2 Koraci analize

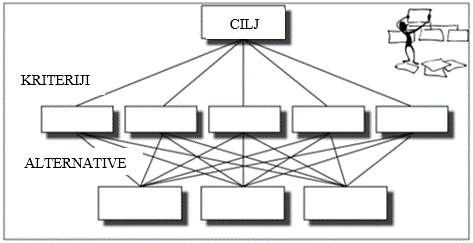
Prvi korak u provedbi modela je rastavljanje problema određivanja prioriteta na hijerarhijske razine (Saaty i Kearns, 1991; Saaty i Vargas, 1991; Saaty i Forman, 1993).  To znači da treba definirati minimalno tri razine odlučivanja: cilj, kriterije i alternative.
Svaki model ima hijerarhijsku strukturu i sastoji se iz više razina. Najvišu razinu na hijerarhijskoj ljestvici ima cilj. Zatim slijede kriteriji, eventalno podkriteriji i alternative. Hijerarhijska struktura modela odlučivanja shematski je prikazana na  Slici 1.


Slika 1. Hijerarhijska struktura modela

Drugi korak je formiranje usporedne matrice za sve hijerarhijske razine (Saaty i Vargas, 1991; Forman, 1990).  Ovaj korak je najvažniji i najosjetljiviji korak u modelu definiranja prioriteta. To je ujedno i jedini subjektivni korak (u slučaju kad ne raspolažemo kvanitificiranim ulaznim parametrima) i ovisi o stručnom znanju, iskustvu i osobnim prioritetima koje definira sam donositelj odluka.  Za svaku razinu potrebno je izvršiti međusobno uspoređivanje i vrednovanje elemenata te razine u odnosu na svaki element više razine. Za ranije definirane tri razine, to znači da će se na razini 2 izvesti uspoređivanje svih postavljenih kriterija u odnosu na zadani cilj, dok će se na razini 3 za sve alternative izvesti međusobno uspoređivanje, odnosno vrednovanje u odnosu na zadane kriterije na razini 2. Da bi se kvantificiralo usporedno ocjenjivanje, potrebno je izvršiti normizaciju. Prijedlog jedne takve normizacije predstavljen je u Tablici 1. (Saaty, 1994; Shen i dr. 1998).
 
 
Tablica 1. Kvantificiranje usporednog ocjenjivanja

Intenzitet važnosti	Definicija	Objašnjenje
1	Jednaka važnost	Dva elementa niže razine su jednako važna u odnosu na element više razine
3	Umjerena važnost	Iskustvo i procjena kažu da je jedan element nešto važniji od drugoga
5	Velika važnost	Iskustvo i procjena kažu da je jedan element mnogo važniji od drugog
7	Veoma velika važnost	Praksa pokazuje da je jedan element veoma važniji od drugoga
9	Ekstremno velika važnost	Činjenice govora da jedan element ima apsolutni prioritet o odnosu na drugi
2,4,6,8	Međuvrijednosti između ranije navedenih	Potreban kompromis i subjektivna prosudba
Recipročno u odnosu na gornje vrijednosti	Ako aktivnost i ima jednu od gornjih vrijednosti u usporedbi s aktivnosću j, onda aktivnost j ima recipročnu vrijednost u usporedbi s aktivnošću i	Ovo je razumna pretpostavka

 
Primjeri korištenja Tablice 1:

• Ako donositelj odluka procjenjuje da je kriterij 1 apsolutno važniji od kriterija 2 s obzirom na postavljeni cilj, tada element matrice ima ocjenu 9.
• Ako donositelj odluke procjenjuje da je alternativa 1 nešto važnija od alternative 2 obzirom na kriterij 2, onda element matrice dobiva vrijednost 3.

Tablica 2. Primjer matrice obzirom na razinu 1

Obzirom na cilj	Kriterij 1	Kriterij 2	Kriterij 3
Kriterij 1	1	3	5
Kriterij 2	1/3	1	4
Kriterij 3	1/5	1/4	1

 
Iz Tablice 2 može se vidjeti da je ocijenjeno da je, na primjer, kriterij 1 umjereno (3) važniji od kriterija 2 obzirom na postavljeni cilj određivanja prioriteta.

Tablica 3. Primjer matrice obzirom na razinu 2

Obzirom na kriterij 2	Alternativa 1	Alternativa 2	Alternativa 3	Alternativa 4	Alternativa 5
Alternativa 1	1	1/3	1/2	1/4	2
Alternativa 2	3	1	2	1/2	4
Alternativa 3	2	1/2	1	1/3	3
Alternativa 4	4	2	3	1	5
Alternativa 5	1/2	1/4	1/3	1/5	1

 
Iz Tablice 3 može se vidjeti da je ocijenjeno da je, na primjer, alternativa 2 umjereno do veoma (4) važnija od alternative 5 obzirom na kriterij 2.
Treći korak je izračunavanje regionalnih svojstvenih vektora i svojstvenih vrijednosti usporednih matrica za sve hijerarhijske razine. Za razinu kriterija regionalni svojstveni vektor težinski definira redoslijed važnosti pojedinih kriterija u postizanju cilja, dok za razinu alternativa regionalni svojstveni vektor definira redoslijed važnosti pojedinih alternativa u odnosu na zadani kriterij.
Da bi se odredio svojstveni vektor i najveća svojstvena vrijednost usporedne matrice mora se riješiti generalni problem svojstvenih vrijednosti koji se zapisuje u obliku (1):

AW = lmaxW

(1)

 
gdje je:
A - usporedna matrica,
W = (W1, W2, W3, W4, W5)^T - svojstveni vektor i
l_max - najveća svojstvena vrijednost.
 
Četvrti korak je izračunavanje koeficijenta konzistencije za svaku usporednu matricu na svim razinama koji se određuje pomoću svojstvene vrijednosti usporedne matrice. Ako je koeficijent konzistencije veći od 0.10, donesene su nekonzistentne prosudbe u formiranju usporednih matrica na pojedinim hijerarhijskim razinama i te se matrice moraju ponovo formirati.  Ako je koeficijent konzistencije manji od 0.10, može se prijeći na slijedeći korak.
Saaty je predložio da se indeks konzistencije CI izračunava prema izrazu (2):

CI = (lmax - n) / (n-1)

(2)

gdje je:
l_max - najveća svojstvena vrijednost usporedne matrice,
n - red usporedne matrice.
 
Koeficijent konzistencije se izračunava prema izrazu (3):

CR = CI / RI

(3)

 
gdje je RI slučajna konzistencija dobivena uprosječenjem indeksa konzistencije slučajno generiranih recipročnih matrica. Vrijednosti RI prikazane su u Tablici 4.
 
Tablica 4. Vrijednosti slučajne konzistencije (RI)

n	1	2	3	4	5	6	7	8	9	10
RI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

 
Peti korak je sintetiziranje rezultata proračuna na svim razinama, te definiranje težina svake alternative u odnosu na postizanje cilja. Proračunava se globalni svojstveni vektor te globalni koeficijent konzistencije. Ako je globalni koeficijent konzistencije veći od 0.10 ponovno egzistiraju nekonzistentne prosudbe, pa se moraju redefinirati usporedne matrice. Ako je koeficijent konzistencije manji od 0.10 završen je proces definiranja težinskih odnosa alternativa u odnosu na postavljeni cilj.
Proračun globalnog svojstvenog vektora predstavlja jednostavnu tehniku težinskog uprosjećivanja. Svojstveni vektori razine 1 pomnoženi sa svojstvenim vektorima nivoa 2, te zbrojeni za svaki kriterij, daju globalni svojstveni vektor.
Proračun globalnog koeficijenta konzistencije provodi se jednostavnim uprosječivanjem regionalnih koeficijenata konzistencije na razinama 1 i 2.
Vrijednost svojstvenog vektora za svaki kriterij predstavlja njegovu težinu pri izračunavanju indeksa prioriteta. Poretkom po vrijednosti indeksa prioriteta definira se lista prioriteta prema postavljenom cilju analize.

3. Primjer procjene potresnog rizika pojedinih geografskih područja

Primjena AHP modela prikazat će se na primjeru procjene potresnog rizika po pojedinim geografskim područjima. Uz pomoć metode AHP-a moguće je usporedbama odrediti listu prioriteta pojedinih četvrti, gradova, županija, zemalja ili sl., prema veličini potresnog rizika. Na taj je način moguće izraditi i prikazati sveobuhvatne mape rizika nekog područja, koje obuhvaćaju sve dimenzije potresnog rizika (potresnu opasnost, izloženost, oštetljivost, ali i troškovne, društvene i druge aspekte potresa). Slične analize gdje se AHP koristi za procjenu potresnog rizika samostalno ili u kombinaciji s ostalim metodama prikazane su u znanstvenim radovima Fariza i dr. (2016), Nyimbili i dr. (2018), Jena i dr. (2020), Jena i Pradhan (2020), Özkazanç i dr. (2020), Shadmaan i Islam (2021).
Kao pomoćni alat u ovoj analizi koristi se računalni program Super Decisions za potporu odlučivanju (Super Decisions, 2022) koji se temelji na AHP metodi.
 
 

3.1 Formiranje hijerarhijskih razina

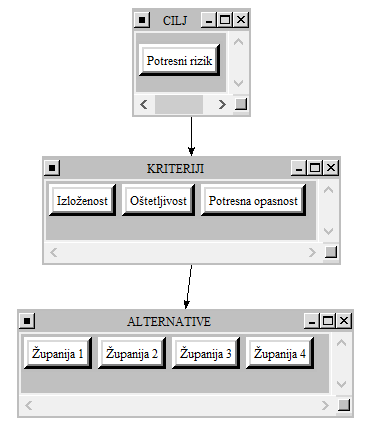
Problem prioriteta pojedinih geografskih područja rastavljen je u tri hijerarhijske razine: cilj, kriteriji i alternative.
Razina 1 uvijek predstavlja postavljeni cilj koji se želi postići analizom, a u ovom se slučaju odnosi na procjenu potresnog rizika. To je najviša hijerarhijska razina čiji prioritet se kvantificira indeksom prioriteta za svaku pojedinu alternativu, odnosno geografsku regiju koju promatramo. U navedenom primjeru cilj je određivanje potresnog rizika na razini države.
Razina 2 sadrži kriterije koji su pretpostavljeni kao važni atributi s obzirom na ispunjavanje cilja na razini 1. Zadavanje tih kriterija predstavlja veoma važan korak, jer se njima moraju obuhvatiti svi važni elementi potresnog rizika. U ovom su primjeru kriteriji:

• potresna opasnost,
• izloženost,
• oštetljivost.

 
Razina 3 daje alternative koje se uspoređuju s obzirom na kriterije na razini 2, a sve u funkciji cilja postavljenog na razini 1. Na razini države, alternative bi mogle biti županije ili gradovi i općine. U ovom primjeru prikazat će se nekoliko proizvoljnih županija, samo u svrhu prezentacije metode:

• Županija 1,
• Županija 2,
• Županija 3,
• Županija 4.

U računalnom programu Super Decisions definiran je tako opisani model (Slika 2).


Slika 2. Model za odlučivanje u programu Super Decisions

3.2 Formiranje usporednih matrica

Nakon definiranja modela s minimalno tri hijerarhijske razine, pristupa se formiranju usporednih matrica. U ovom primjeru postoje četiri usporedne matrice, odnosno jedna u odnosu na razinu 1 (razina cilja) i tri u odnosu na razinu 2 (razina kriterija). Broj usporedbi koje je potrebno napraviti unutar svake matrice iznosi n(n-1)/2, ako je n broj definiranih kriterija, odnosno alternativa. U ovom je primjeru ocjenjivanje provedeno na temelju normizacije iz Tablice 1.
U Tablici 5 prikazana je usporedna matrica s obzirom na razinu 1, u kojoj su međusobno uspoređeni definirani kriteriji. Važnost pojedinih kriterija u odnosu na definirani cilj određuje donositelj odluka. Takve su odluke subjektivne, ali temeljene na činjenicama koje su donositelju odluka dostupne u trenutku analize.
 
Tablica 5. Usporedna matrica s obzirom na razinu 1

Obzirom na cilj	Potresna opasnost	Izloženost	Oštetljivost
Potresna opasnost	1	3	5
Izloženost	1/3	1	4
Oštetljivost	1/5	1/4	1

 
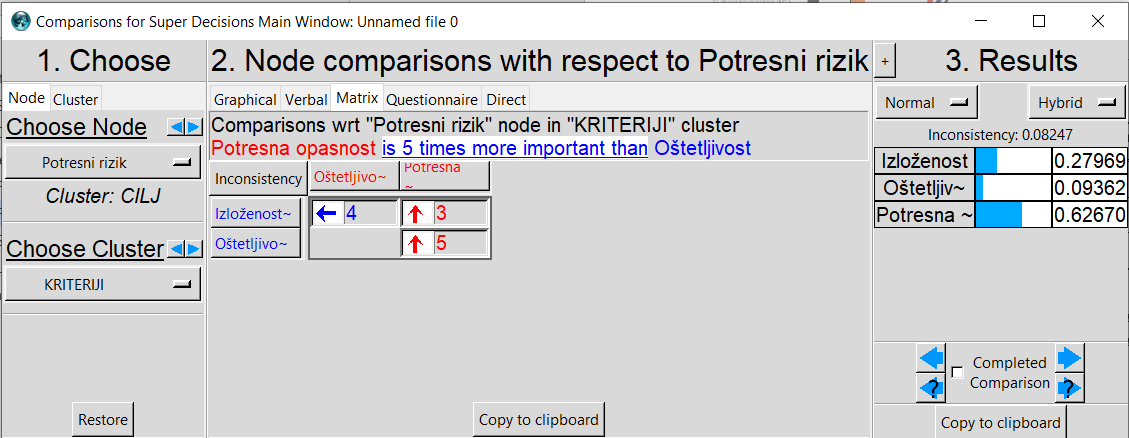
Iz Tablice 5 može se vidjeti da je ocijenjeno da je, na primjer, potresna opasnost umjereno važnija od izloženosti obzirom na određivanje potresnog rizika na razini države. Na Slici 3 prikazan je isječak iz programa Super Decisions, gdje se automatski izračunava i vrijednost svojstvenog vektora Wk te koeficijenta konzistencije CRk za razinu 1:
W_k = (W1, W2, W3)^T = (0.280, 0.094, 0.627)^T
CR_k = 0.082 < 0.10


Slika 3. Usporedba kriterija u odnosu na cilj – Super Decisions
 
U Tablici 6 prikazana je jedna usporedna matrica s obzirom na razinu 2, u kojoj su međusobno uspoređene definirane alternative s obzirom na kriterij potresne opasnosti. Važnost pojedinih alternativa u odnosu na kriterij potresne opasnosti može se donijeti na temelju ulaznih podataka o potresnoj opasnosti na području svake županije. Prilikom međusobne usporedbe, veće ocjene dobiva županija na čijem je području potresna opasnost veća, odnosno veći su potencijalni razorni učinci potresa (primjerice podrhtavanje tla, likvefakcija, odroni, tsunami i slično) na promatranoj lokaciji.
 
Tablica 6. Usporedna matrica s obzirom na razinu 2 – kriterij potresne opasnosti

Obzirom na potresnu opasnost	Županija 1	Županija 2	Županija 3	Županija 4
Županija 1	1	1	5	3
Županija 2	1	1	5	3
Županija 3	1/5	1/5	1	1/3
Županija 4	1/3	1/3	3	1

 
Iz Tablice 6 može se vidjeti kako je ocijenjeno da je, na primjer, u Županiji 1 potresna opasnost znatno veća (5) nego u Županiji 3. Na Slici 4 prikazan je isječak iz programa Super Decisions, gdje se automatski izračunava i vrijednost svojstvenog vektora Wa1 te koeficijenta konzistencije CR_a1 za razinu 2:
W_a1 = (W₁, W₂, W₃, W₄)^T = (0.390, 0.390, 0.068, 0.152)^T
CR_a1 = 0.016 < 0.10


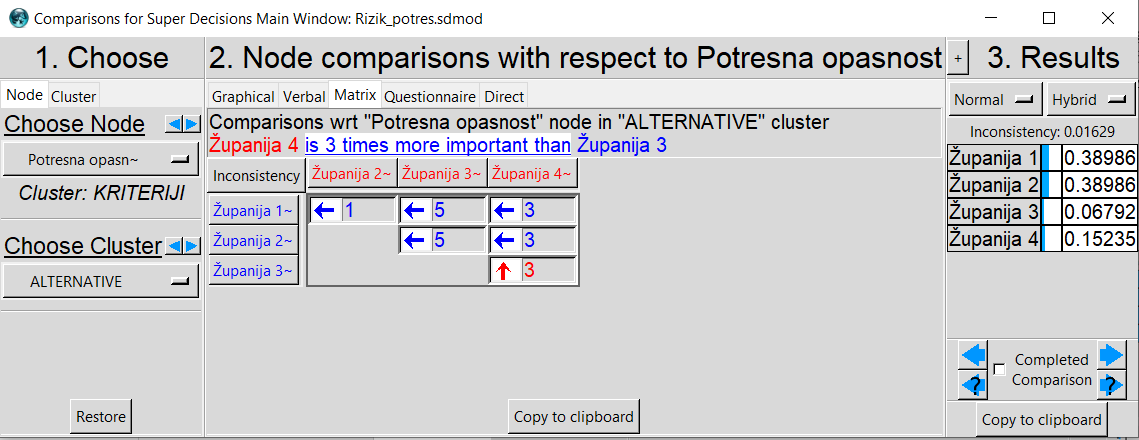
Slika 4. Usporedba alternativa u odnosu na kriterij potresne opasnosti – Super Decisions

U Tablici 7 prikazana je jedna usporedna matrica s obzirom na razinu 2, u kojoj su međusobno uspoređene definirane alternative s obzirom na kriterij izloženosti izgrađenog okoliša. Važnost pojedinih alternativa u odnosu na kriterij izloženosti može se donijeti na temelju ulaznih podataka o izloženosti na području svake županije. Prilikom međusobne usporedbe, veće ocjene dobiva županija na čijem je području izloženost izgrađenog okoliša veća, odnosno veći su gubitci uslijed potresa povezani s izgrađenim okolišem.

Tablica 7. Usporedna matrica s obzirom na razinu 2 – kriterij izloženosti

Obzirom na izloženost	Županija 1	Županija 2	Županija 3	Županija 4
Županija 1	1	1/5	1/2	1/3
Županija 2	5	1	7	3
Županija 3	2	1/7	1	1/3
Županija 4	3	1/3	3	1

 
Iz Tablice 7 može se vidjeti da je ocijenjeno da je, na primjer, u Županiji 2 izloženost građevina veoma veća (7) nego u Županiji 3. Na Slici 5 prikazan je isječak iz programa Super Decisions, gdje se automatski izračunava i vrijednost svojstvenog vektora Wa2 te koeficijenta konzistencije CR_a2 za razinu 2:
W_a2 = (W₁, W₂, W₃, W₄)^T = (0.079, 0.583, 0.102, 0.236)^T
CR_a2 = 0.046 < 0.10
 

Slika 5. Usporedba alternativa u odnosu na kriterij izloženosti – Super Decisions
 
U Tablici 8 prikazana je jedna usporedna matrica s obzirom na razinu 2, u kojoj su međusobno uspoređene definirane alternative s obzirom na kriterij oštetljivosti. Važnost pojedinih alternativa u odnosu na kriterij oštetljivosti može se donijeti na temelju ulaznih podataka o oštetljivosti izgrađenog fonda građevina na području svake županije. Prilikom međusobne usporedbe, veće ocjene dobiva županija na čijem je području oštetljivost izgrađenog okoliša veća, odnosno konstrukcijske značajke izloženih građevina su takve da su one podložnije učincima potresa (oštećenjima).
 
 
Tablica 8. Usporedna matrica s obzirom na razinu 2 – kriterij oštetljivosti

Obzirom na izloženost	Županija 1	Županija 2	Županija 3	Županija 4
Županija 1	1	2	4	3
Županija 2	1/2	1	3	4
Županija 3	1/4	1/3	1	1
Županija 4	1/3	1/4	1	1

 
Iz Tablice 8 može se vidjeti da je ocijenjeno da je, na primjer, u Županiji 3 oštetljivost građevina jednaka kao i u Županiji 4. Na Slici 6 prikazan je isječak iz programa Super Decisions, gdje se automatski izračunava i vrijednost svojstvenog vektora W_a3 te koeficijenta konzistencije CR_a3 za razinu 2:
W_a3 = (W₁, W₂, W₃, W₄)^T = (0.458, 0.323, 0.108, 0.111)^T
CR_a3 = 0.031 < 0.10
 

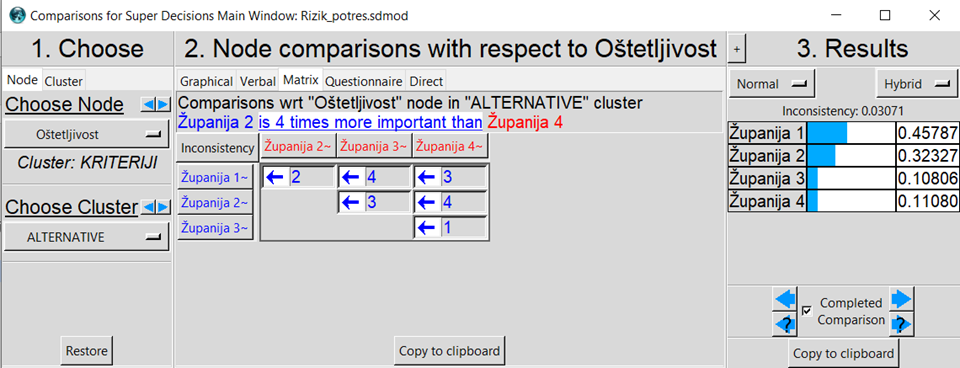Slika 6. Usporedba alternativa u odnosu na kriterij oštetljivosti – Super Decisions
 

3.3 Sinteza rezultata

Nakon što su sve usporedne matrice definirane, proračunava se globalni svojstveni vektor, koji označava težinu u određivanju prioriteta alternativa.
Proračun globalnog svojstvenog vektora predstavlja jednostavnu tehniku težinskog uprosječivanja. Svojstveni vektori razine 1 pomnoženi sa svojstvenim vektorima razine 2, te zbrojeni za svaku alternativu, daju globalni svojstveni vektor. Rezultati AHP-a prikazani su na Slici 7, sa globalnim svojstvenim vektorom prikazanim u srednjem stupcu.
 

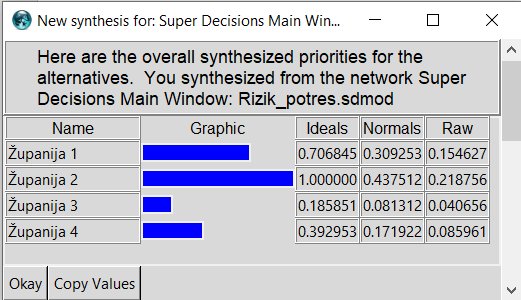
Slika 7. Rezultati AHP-a za potresni rizik županija

Prema rezultatima AHP-a, relativne težine svake alternative (W), odnosno indeksi njihovog potresnog rizika, iznose:
W (Županija 1) = 0.309
W (Županija 2) =  0.438
W (Županija 3) = 0.081
W (Županija 4) = 0.172
Ovakvi rezultati mogu se interpretirati i lingvistički, ako se za pojedine vrijednosti težina alternativa dodijele značenja poput: vrlo mali, mali, srednji, visoki, vrlo visoki rizik. Prema tome, Županija 2 ima visok potresni rizik, Županija 1 srednji potresni rizik, a Županije 3 i 4 imaju mali potresni rizik. Isto se može interpretirati i bojama ili na bilo koji drugi sličan način. Na karti se tako vrlo jasno može prikazati potresni rizik pojedinih županija, koji uzima u obzir sve elemente potresnog rizika. Primjer jednog takvog prikaza može se vidjeti na Slici 8.
 

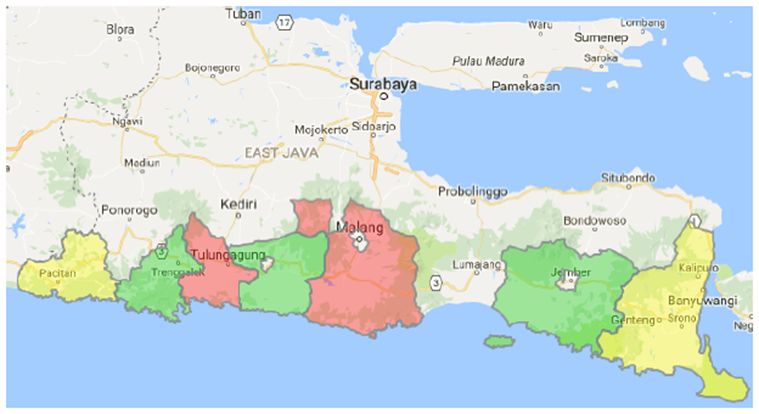Slika 8. Potresni rizik po geografskim regijama: crveno – visok rizik; žuto – srednji rizik; zeleno – mali rizik (Fariza i dr., 2016)

4. Zaključak

U ovom je izvješću prikazan primjer korištenja analitičkog hijerarhijskog procesa za analizu i evaluaciju potresnog rizika. Pokazano je kako se upotrebom AHP-a mogu objediniti različiti elementi potresnog rizika i sveobuhvatno prikazati razinu potresnog rizika pojedine geografske regije. Isto se može primijeniti na razini svijeta, kontinenta, države, županija, gradova i općina. U sljedećim izvješćima napravit će se rekapitulacija pregleda postojećeg stanja i započeti s definiranjem koraka metodologije za procjenu rizika koja će biti primjenjiva na Zagreb, ali i cjelokupno područje RH.

5. Literatura

Fariza, A., Abhimata, N.P., Hasim, J.A.N. (2016) 'Earthquake Disaster Risk Map in East Java, Indonesia, using Analytical Hierarchy Process – Natural Break Classification', u: 2016 International Conference on Knowledge Creation and Intelligent Computing (KCIC), 15-17 November, Manado, Indonesia. IEEE.
Forman, E.H., (1990) 'Random Indices for Incomplete Pairwise Comparison Matrices', European Journal of Operations Research, 48(1), 153-155.
Jena, R., Pradhan, B. (2020) ' Earthquake Risk Assessment Using Integrated Influence Diagram–AHP Approach', IOP Conf. Series: Earth and Environmental Science, 540, 012078.
Jena, R., Pradhan, B., Beydoun, G., Nizamuddin, Ardiansyah, Sofyan, H., Affan, M. (2020) 'Integrated model for earthquake risk assessment using neural network and analytic hierarchy process: Aceh province, Indonesia', Geoscience Frontiers, 11, 613-634.
Nyimbili, P.H., Erden, T., Karaman, H. (2018) 'Integration of GIS, AHP and TOPSIS for earthquake hazard analysis', Natural Hazards, 92, 1523–1546.
Özkazanç, S., Sıddıquı, S.D., Güngör, M. (2020) 'Sensitivity Analysis of Earthquake Using the Analytic Hierarchy Process (AHP) Method: Sample of Adana', Idealkent Dergisi (Journal of Urban Studies), 11(30), 570-591.
Saaty, T.L. (1992) Multicriteria Decision Making - The Analytic Hierarchy Process, RWS Publications, 4922 Ellsworth Ave., Pittsburgh, PA 15213. Vol. I, AHP Series.
Saaty, T.L. (1994) Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process, RWS Publications, 4922 Ellsworth Ave., Pittsburgh, PA 15213. Vol. VI, AHP Series.
Saaty, T.L., Alexander, J.M. (1989) Conflict Resolution - The Analytic Hierarchy Process, Praeger, NY.
Saaty, T.L., Forman, E. (1993) The Hierarchon, RWS Publications, 4922 Ellsworth Ave.,Pittsburgh, PA, 15213. Vol. V, AHP Series.
Saaty, T.L., Kearns, K. (1991) Analytical Planning, RWS Publications, 4922 Ellsworth Ave., Pittsburgh, PA 15213. Vol. IV, AHP Series.
Saaty, T.L., Vargas, L. G. (1991) Prediction, Projection and Forecasting, Kluwer Academic Publishers, Boston, Mass.
Shadmaan, S., Islam, A.I. (2021) 'Estimation of earthquake vulnerability by using analytical hierarchy process', Natural Hazards Research, 1, 153–160.
Shen, Q., Lo, K.-K., Wang, Q. (1998) 'Priority Setting in Maintenance Management of Public Building - A Modified Multi-Attribute Approach Using AHP', Construction Management and Economics, 16, 693-702.
Super Decisions (2022) Super Decisions CDF [Online]. Dostupno na: https://www.superdecisions.com (pristupljeno: 1. prosinca 2022.).